Ambisonic Transcoding
Default transcoding
When patching an HOA or B-Format input to a source, or an HOA room to a channel-based output, a transcoder will be automatically inserted. This transcoder will, by default, be set to the Ring or Sloane speaker arrangement corresponding to the HOA order, and, will select an AllRad decoder.
Ring and Sloane are uniform setups that are recommended for optimized transcoding. It will guarantee precise localization, in particular when transcoding an ambisonic input in order to use it in a room.
Transcoding method
Projection
Projection decoding is also sometimes called “sampling ambisonic decoding” (SAD). It is the simplest form of ambisonic decoding. It samples the virtual panning function at the loudspeaker directions. SAD is optimal for loudspeakers arranged as t-design layouts, with t ≥ (2N+1) ( N being the Ambisonics order). Typically, the SAD should only be used for 2D loudspeaker layouts, i.e., regularly arranged in a circle. Avoids this decoder for 3D setups.
What is a T-Design Layout?
To keep it really simple, t-design is a mathematical way of constructing sphere perimeters or circle surfaces with an array of points that is homogenous. In 2D the point simply put on a circle and are evenly spaced. In 3D, things get much more complicated many T-design point layouts exist. In SPAT Revolution, we chose to use the method used by the mathematician Sloane for our speaker layouts.
Regularized pseudo-inverse
The pseudo-inverse decoder, or “mode-matching decoder” (MMAD), is suitable for both 2D and 3D. It is based on a pseudo-inverse of the re-encoding matrix. MMAD is well-behaved for regular loudspeaker arrangements. It can also give good results with slightly irregular setups. However, it can become unstable with strongly irregular setups, i.e., it can completely blow up the speaker feeds. So, be careful.
The regularized pseudo-inverse decoder or “regularized-mode-matching decoder” (RMMAD) is somehow similar to MMAD. However, it uses a regularization factor for the stabilization of the pseudo-inverse. This regularization factor (alpha) varies from 0% to 100%. A value of 0% provides results similar to MMAD. A value of 100% generates even energy distribution, i.e., results similar to EPAD. Intermediate values of alpha allow to “blend” MMAD and EPAD.
Energy preserving
EPAD (energy-preserving ambisonic decoding) and AllRAD (All-round Ambisonic decoding) are other HOA decoding methods suitable for 2D and 3D HOA, and they can cope with any kind of loudspeaker arrangement. These decoding methods always work, as soon as there are enough loudspeakers; they are always feasible and by nature numerically stable. EPAD uses a regularized matrix inversion such that the decoded energy is preserved even with non-uniformly arranged arrays (and even for directions with only sparse loudspeaker coverage). EPAD is the default method in spat5 (and the one we usually recommend).
AllRAD
“All-round Ambisonic decoding” (AllRAD) is designed in two steps. First, an optimal virtual loudspeaker layout using T-design arrangement is considered (for which the SAD is optimal). Secondly, the signals of these virtual loudspeakers are mapped to the real loudspeakers via VBAP.
Improved AllRAD
“Improved All-Round Ambisonic Decoding” (AllRAD+) combines AllRAD and SAD. Constant energy that is achieved for the idealized virtual loudspeaker setup in AllRAD is corrupted by the VBAP stage as, per loudspeaker pair, all virtual sources are superimposed linearly instead of energetically. The prevailing linear superposition increases the energy wherever the loudspeaker spacing is large. Roughly, at such directions AllRAD doubles the energy, whereas it is halved at directions with dense loudspeaker spacing. Conversely, SAD might lose all energy where the loudspeaker spacing is large and roughly doubles it where the loudspeaker spacing is dense. AllRAD+ tries to solve this issue by combining (i.e., mixing) SAD and AllRAD. The loudness variation of AllRAD+ is competitive with EPAD and its angular mapping resembles AllRAD.
Transcoding types
To improve the ambisonic render, there are some strategies that can be applied at the decoding stage. The idea is to optimize the phase or the energy to improve sound localization.
Basic
This is the standard way to decode ambisonic, and no optimization is applied.
InPhase
The audio content will be optimized in phase, for the all spectrum.
MaxRe
The energy of the audio content will be optimized, for the all spectrum.
BasicMaxRe
The low end of the audio content is not optimized, but a MaxRe method is applied to the high end. The crossover frequency is by default set to 700 Hz.
MaxReInPhase
The low end of the audio content is optimized in energy (MaxRe), but a in-phase method is applied to the high end. The crossover frequency is by default set to 700 Hz.
InPhaseMaxRe
As phase optimization is more efficient in the low frequencies, and energy optimization is prominent in the high frequencies, this method takes this phenomenon to its advantage by splitting the signal into two frequency bands. The crossover frequency is by default set to 700 Hz and can be adjusted.
Basic rules of thumb when transcoding ambisonic to speaker
Ambisonic order and number of speakers
There is a direct relationship between the ambisonic order and the number of loudspeakers we want to use. There must always be at least as many loudspeakers as there are ambisonic channels. For example, first-order ambisonic encapsulates 4 channels and second-order ambisonic encapsulates 9 channels. So we should use first-order ambisonic for a 3D array of up to 8 loudspeakers, then move on to second-order ambisonic. We could continue to use second order until our loudspeaker array grows to use more than 15 loudspeakers. We can continue this way of thinking up to 7th order ambisonic.
How to handle multiple renderings from a single ambisonic room
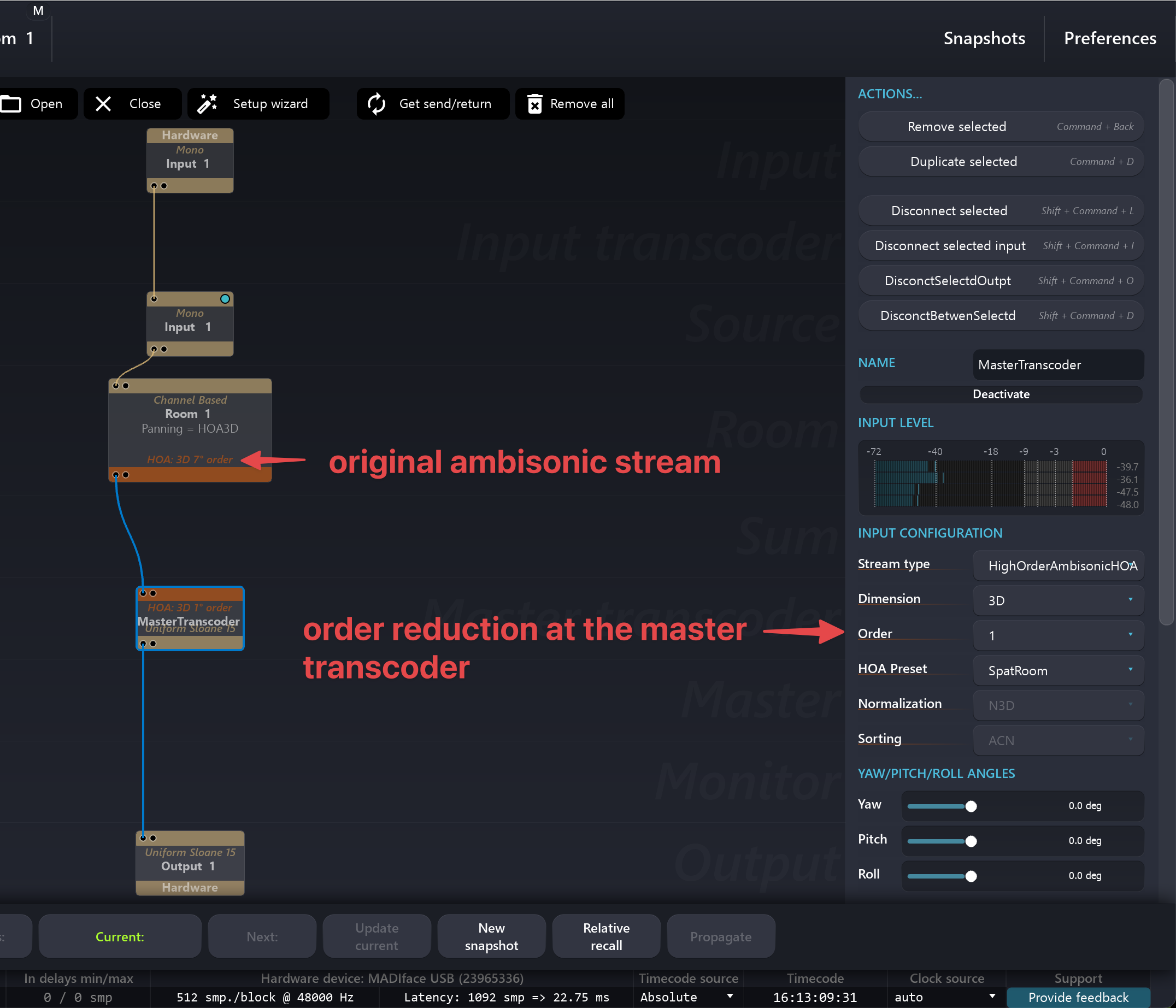
An example of an ambisonic workflow would be to use a 7th-order room and then decode it to the desired loudspeaker array. As mentioned before, we need to adjust the ambisonic order depending on the number of loudspeakers. It is possible to reduce the ambisonic order by changing the order of the input stream in the master transcoder. When this is done, higher-order channels will not affect the rendering.
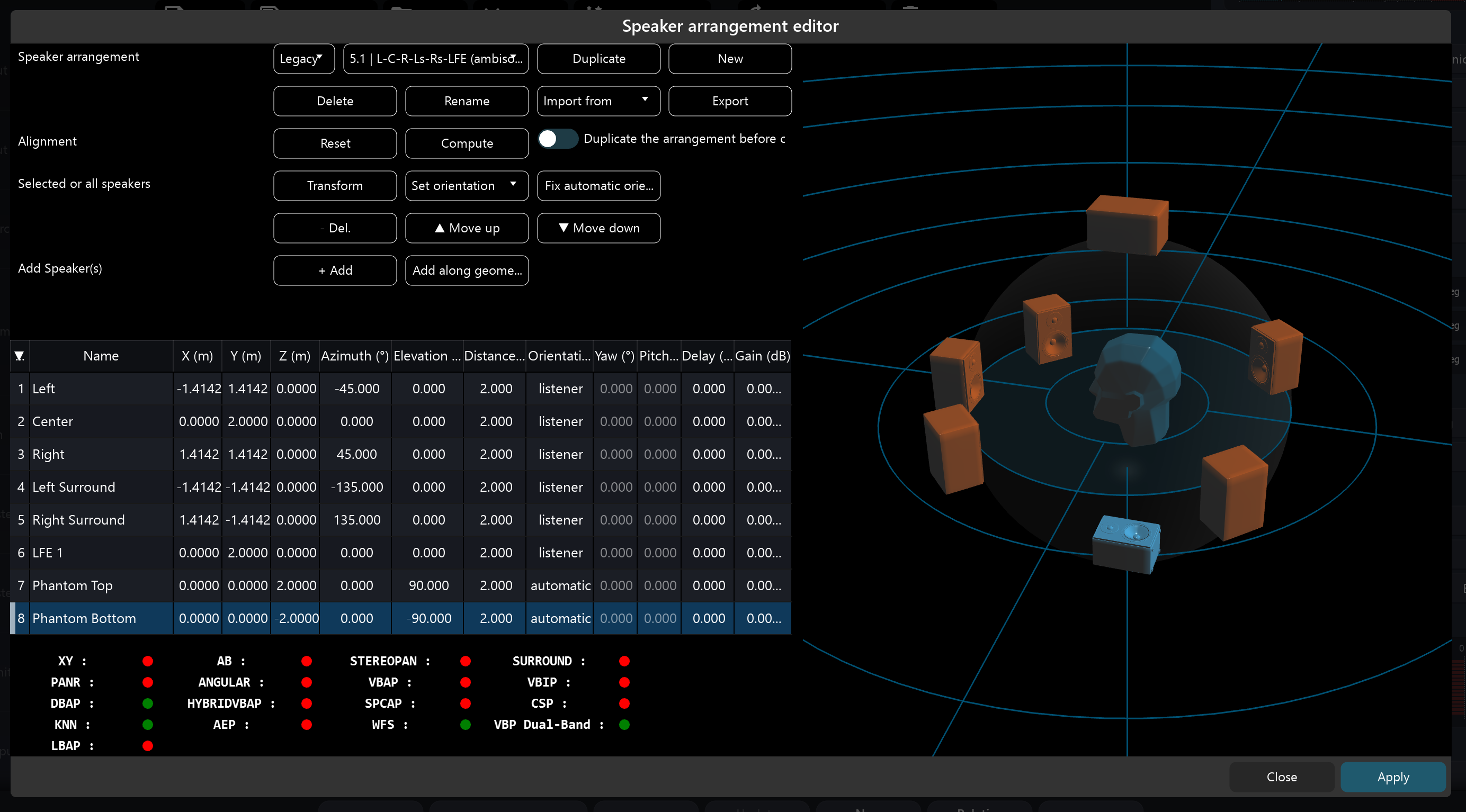
If we want to transcode a 3D ambisonic stream to a 2D speaker layout, one solution is to use two phantom speakers, one at the top and one at the bottom. For example, we could use the speaker layout shown below to transcode a 3D ambisonic scene into a 5.1 layout. It’s important to note that this method will fade out the element that had elevation.
Phantom speakers must be taken into account when determining the appropriate ambisonic order.
We can then have as many transcoders as we like, each dedicated to a specific loudspeaker layout and each adjusting the ambisonic stream accordingly.